题目
假设你正在爬楼梯。需要 n 步你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
1 | 输入: 2 |
示例 2:
1 | 输入: 3 |
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
1 | Input: 2 |
Example 2:
1 | Input: 3 |
解题方法
总台阶数为n,记爬到楼顶的方法数为f(n)。逆向思维,从后往前看,当最后一次爬了一个台阶,则前n-1个台阶有f(n-1)种方法爬完;当最后一次爬了两个台阶,则前n-2个台阶有f(n-2)种方法爬完。则有f(n)=f(n-1)+f(n-2),其中f(1)=f(2)=1,那么这道题便是一道标准的Fibonacci问题。可以有递归和迭代两种方法。
递归
直接上代码,这段代码时间复杂度为O(1.68^n),空间复杂度为O(n),效率低且耗内存,但其代码十分简洁。因为它的效率非常低,就不在leetcode上跑了,肯定会超时。
1 | public class Solution { |
迭代
递归与迭代实际上都是一种分治策略,将复杂的问题分解为简单的问题,区别在于迭代利用了动态规划,将已经计算过的简单的问题的结果进行了保存,减少了不必要的重复计算。这段代码时间复杂度为O(n),空间复杂度为O(1),跑了3ms,超过了77.94%的java提交。
1 | class Solution { |
矩阵
在计算斐波纳契数,分析算法复杂度看到了一种利用矩阵的快速方法,我们可以将Fibonacci转化为求矩阵的幂:
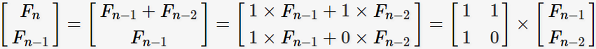
图源:GoCalf Blog
一直递推,可以得到:
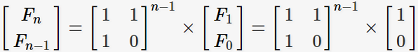
图源:GoCalf Blog
便将问题转化为了求矩阵的n-1次幂了,再利用分治策略,问题的时间复杂度便为O(logn):
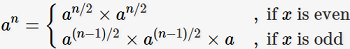
图源:GoCalf Blog
可以利用python的numpy包来进行矩阵的快速运算。

