题目
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(Int) 和其邻居的列表(list[Node])。
示例:
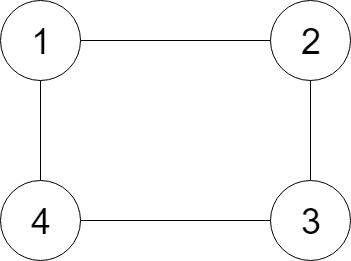
1 | 输入: |
提示:
- 节点数介于 1 到 100 之间。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 必须将给定节点的拷贝作为对克隆图的引用返回。
Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
Example:

1 | Input: |
Note:
- The number of nodes will be between 1 and 100.
- The undirected graph is a simple graph#Simple_graph), which means no repeated edges and no self-loops in the graph.
- Since the graph is undirected, if node p has node q as neighbor, then node q must have node p as neighbor too.
- You must return the copy of the given node as a reference to the cloned graph.
解题方法
BFS
广度优先搜索,用一个队列保存节点的邻居,用一个Map来保存遍历过的节点。
首先克隆传入的节点,然后从非空队列中取出节点,遍历节点的邻居节点,如果邻居节点没有被访问(被克隆),则添加邻居节点到队列中并克隆该邻居节点,然后向当前节点的克隆节点的neighbors添加邻居节点的克隆节点;如果邻居节点已经被访问(被克隆),则直接向当前节点的克隆节点的neighbors添加邻居节点的克隆节点。
这段代码跑了3ms,超过了96.38%的Java提交。
1 | public class Solution { |
DFS
深度优先搜索,使用一个map保存节点与其克隆,用来判断节点是否被克隆,递归调用cloneGraph进行深度优先搜索。这段代码跑了3ms,超过了96.38%的Java提交。
1 | public class Solution { |

